

Pengukuran atau mengukur adalah proses membandingkan suatu besaran dengan besaran sejenis dan ditetapkan sebagai satuan.
x = hasil pengukuran
`\bar{x}`= nilai yang mendekati kebenaran dari nilai rata-rata beberapa data pengukuran
`\Deltax`= ketidakpastian mutlak
(`\Deltax=\frac{1}{2}`)
Hasil pengukuran = skala utama + (skala nonius x tingkat ketelitian)
Hasil pengukuran = skala utama + (skala nonius x tingkat ketelitian)
Hasil pengukuran = skala utama + (skala nonius x tingkat ketelitian)
Besaran Vektor adalah besaran yang memiliki besara (nilai) dan juga arah, misalnya gaya, kecepatan, dan percepatan.
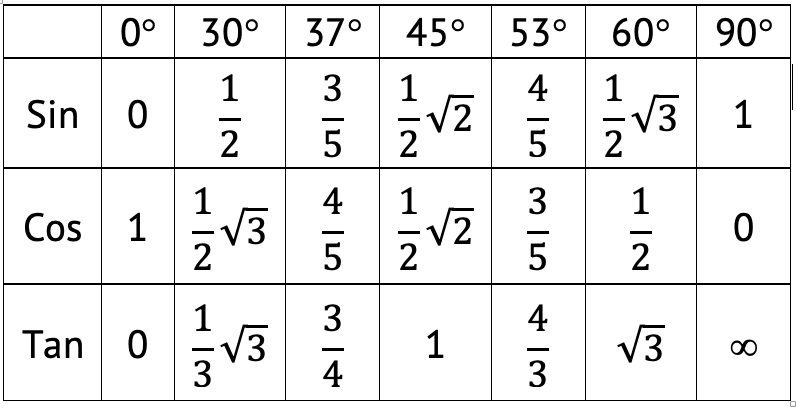
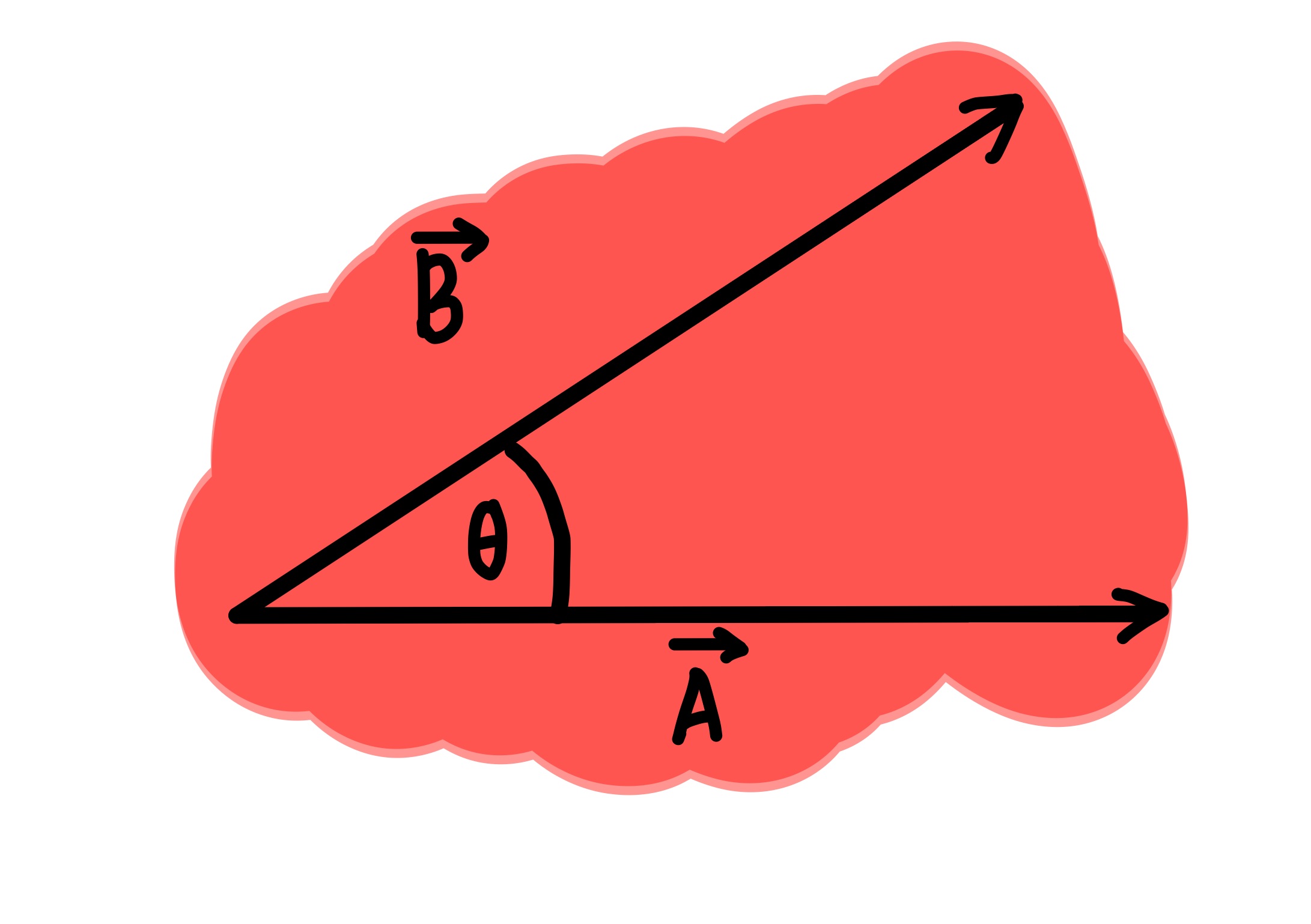
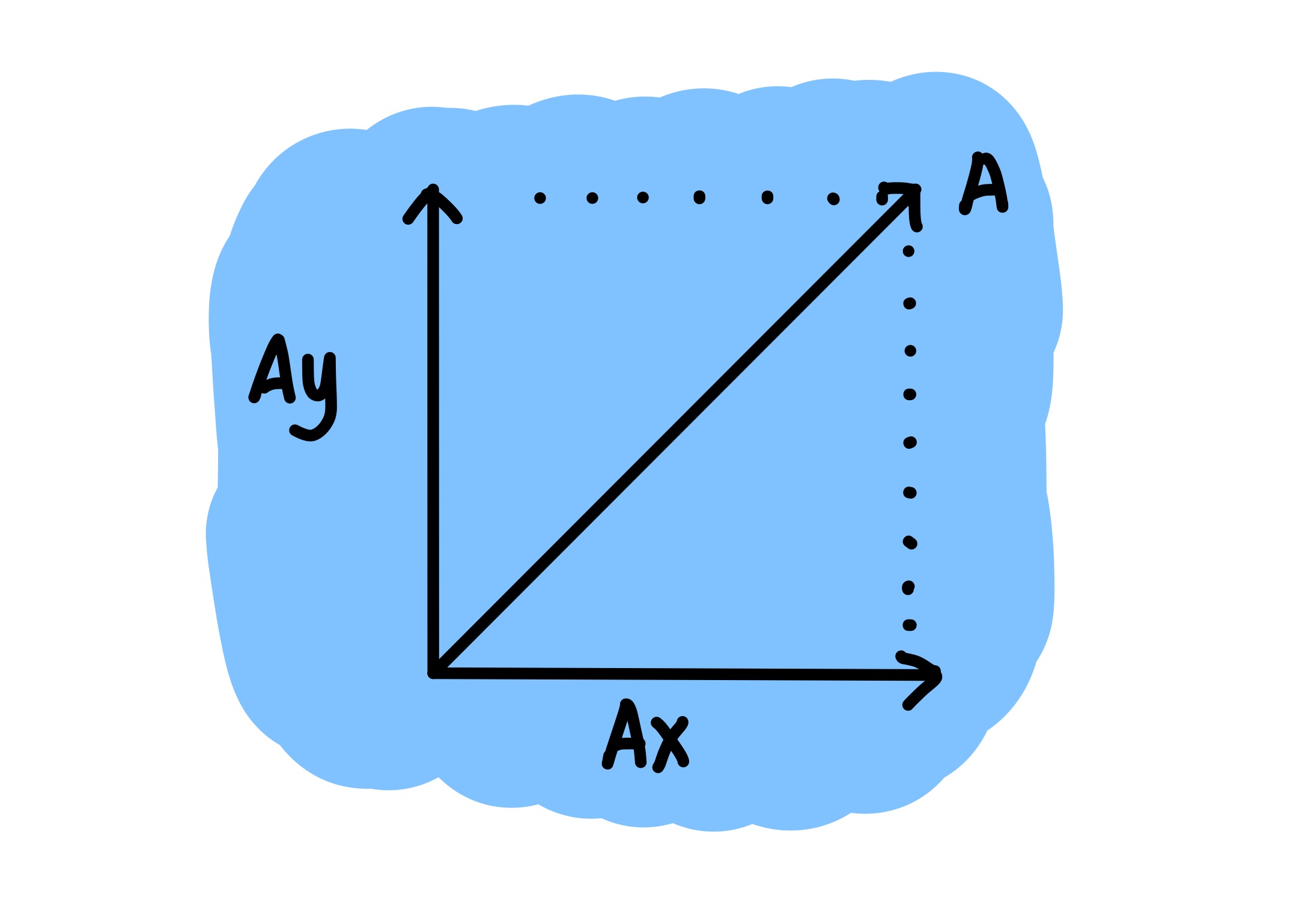
`\sum {R_{x}}^{2}`= Jumlah komponen vektor di Sumbu X.
`\sum {R_{y}}^{2}`= Jumlah komponen vektor di Sumbu Y.
Gerak Lurus merupakan gerakan sebuah benda/partikel dalam lintasan lurus. Dalam mempelajari gerak lurus,
kita akan membaginya dalam dua bagian, yakni gerak lurus pada lintasan horizontal dan gerak lurus pada lintasan vertikal.
`r_{2}`= posisi akhir (m)
`r_{1}`= posisi awal (m)
`t_{2}` = waktu akhir (s)
`t_{1}` = waktu awal (s)
Atau,
v = kecepatan atau kelajuan (m/s)
s = jarak atau perpindahan (m)
t = waktu tempuh (s)
`v_{o}`= kecepatan awal (m/s)
`v_{t}`= kecepatan pada waktu t sekon (m/s)
t = waktu (s)
a = percepatan (m/`s^{2}`)
s = jarak atau perpindahan (m)
`v_{o}`= kecepatan awal (m/s)
`v_{t}`= kecepatan pada waktu t sekon (m/s)
t = waktu (s)
g = percepatan gravitasi (m/`s^{2}`)
h = ketinggian (m)
Gerak Parabola merupakan perpaduan dari dua jenis gerak yaitu, GLB dalam arah horizontal dan GLBB dalam arah vertikal.
Kecepatan :
Posisi :
Kecepatan :
Posisi :
`v_{x}` = kecepatan benda di sumbu x (m/s)
`v_{y}` = kecepatan benda di sumbu y (m/s)
`v_{0}` = kecepatan awal benda
t = waktu (s)
g = percepatan gravitasi (m/`s^{2}`)
`\alpha` = sudut elevasi
x = jarak mendatar
Rumus Titik Tertinggi
Waktu untuk mencapai titik tertinggi :
Rumus Titik Terjauh
Waktu untuk mencapai titik terjauh :
s = panjang busur lingkaran (m)
R = jari-jari lingkaran (m)
Satuan dari posisi sdutu adalah radian, putaran, atau derajat (1 putaran = `360^{\circ}`= `2\pi` rad)
Satuan dari kecepatan sudut adalah rad/s atau rpm.
1 rpm = `\frac{\pi}{30}`rad/s
`\theta_{2}`= posisi sudut akhir (rad)
`\theta_{1}`= posisi sudut awal (rad)
Dengan `\omega` = kecepatan sudut
n = jumlah putaran
t = waktu (sekon)
f = frekuensi (Hz)
T = periode (s)
n = jumlah putaran
t = waktu (sekon)
Maka,
Atau
`\omega` = kecepatan angular
f = frekuensi (Hz)
T = periode (s)
v = kecepatan linear
`\omega` = kecepatan angular
r = jari-jari lintasan
T = periode (s)
f = frekuensi (Hz)
`a_{s}`= percepatan sentripetal (m/`s^{2}`)
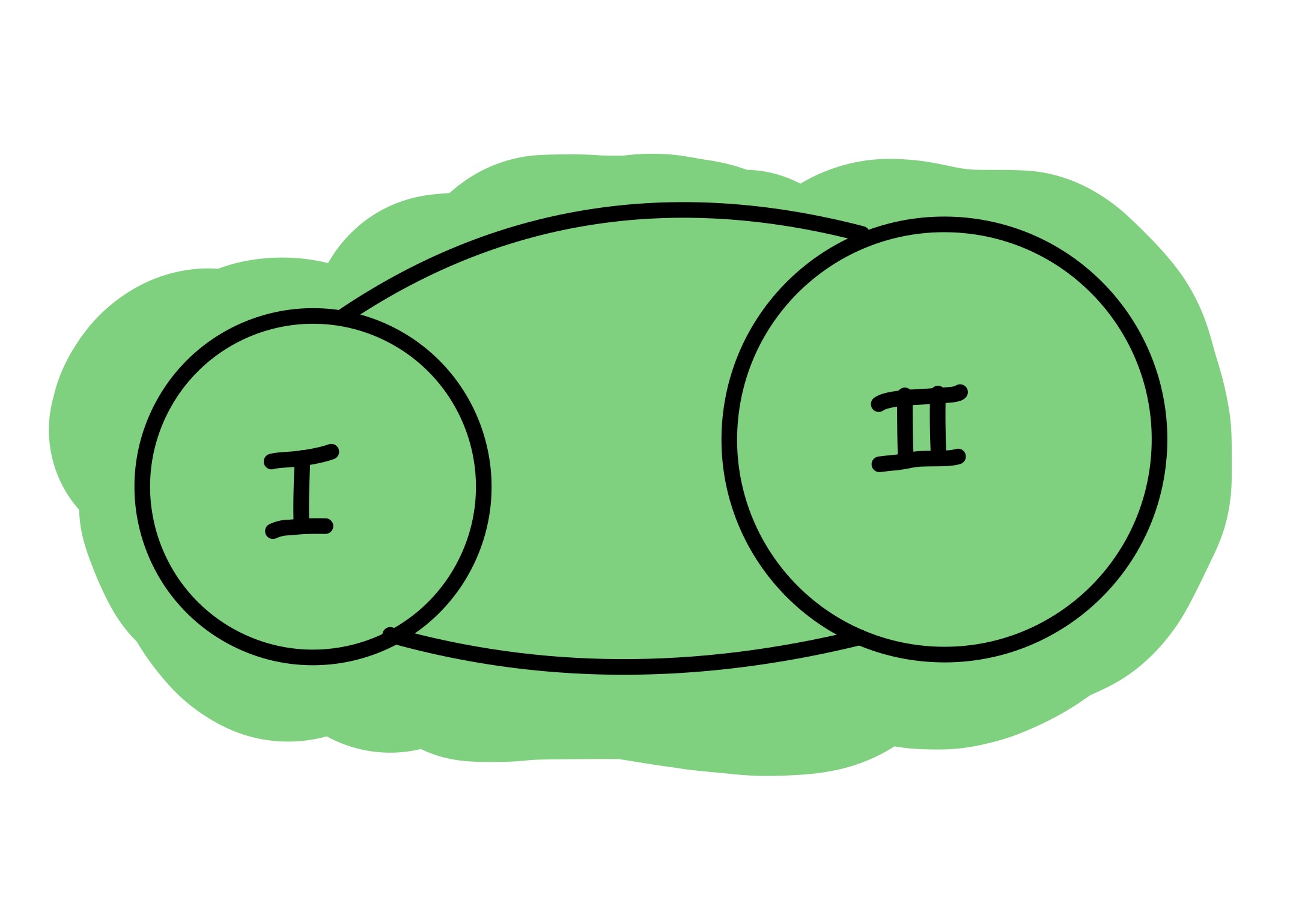
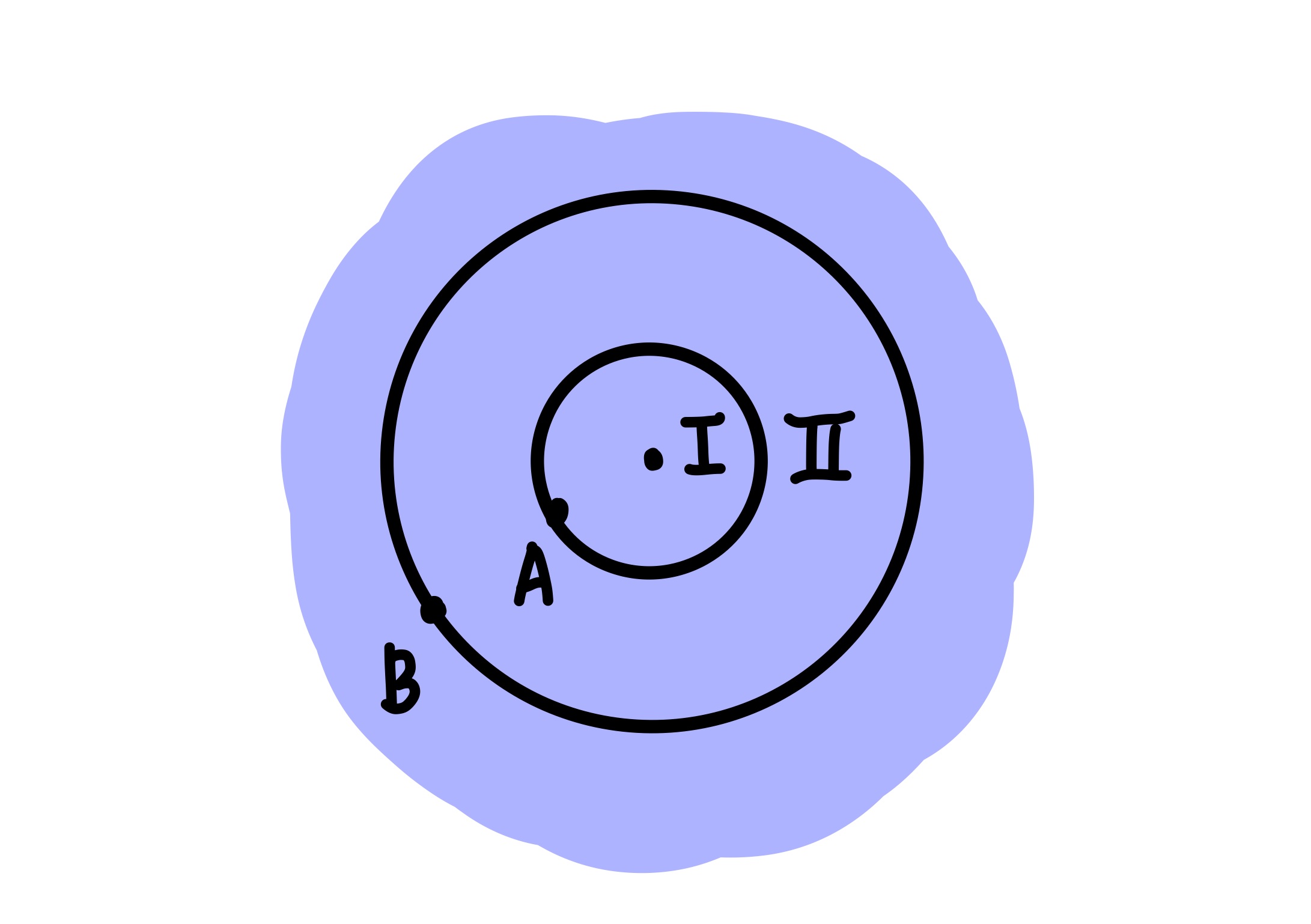
Dinamika merupakan cabang ilmu Fisika yang mempelajari penyebab benda bergerak. Benda dapat bergerak karena ada gaya yang bekerja pada benda tersebut.
`\sumF` = resultan gaya (N)
`\sumF` = resultan gaya (N)
m = massa (kg)
a = percepatan (m/`s^{2}`)
w = gaya berat
m = massa benda (kg)
g = percepatan gravitasi `(m/s^{2})`
N = tegak lurus dengan bidang yang bersentuhan
Jika `F < f_{gs}` maka benda diam (f = F)
Jika `F = f_{gs}` maka benda tepat akan bergerak (f = F)
Jika `F > f_{gs}` maka benda bergerak (f=`f_{gk}`)
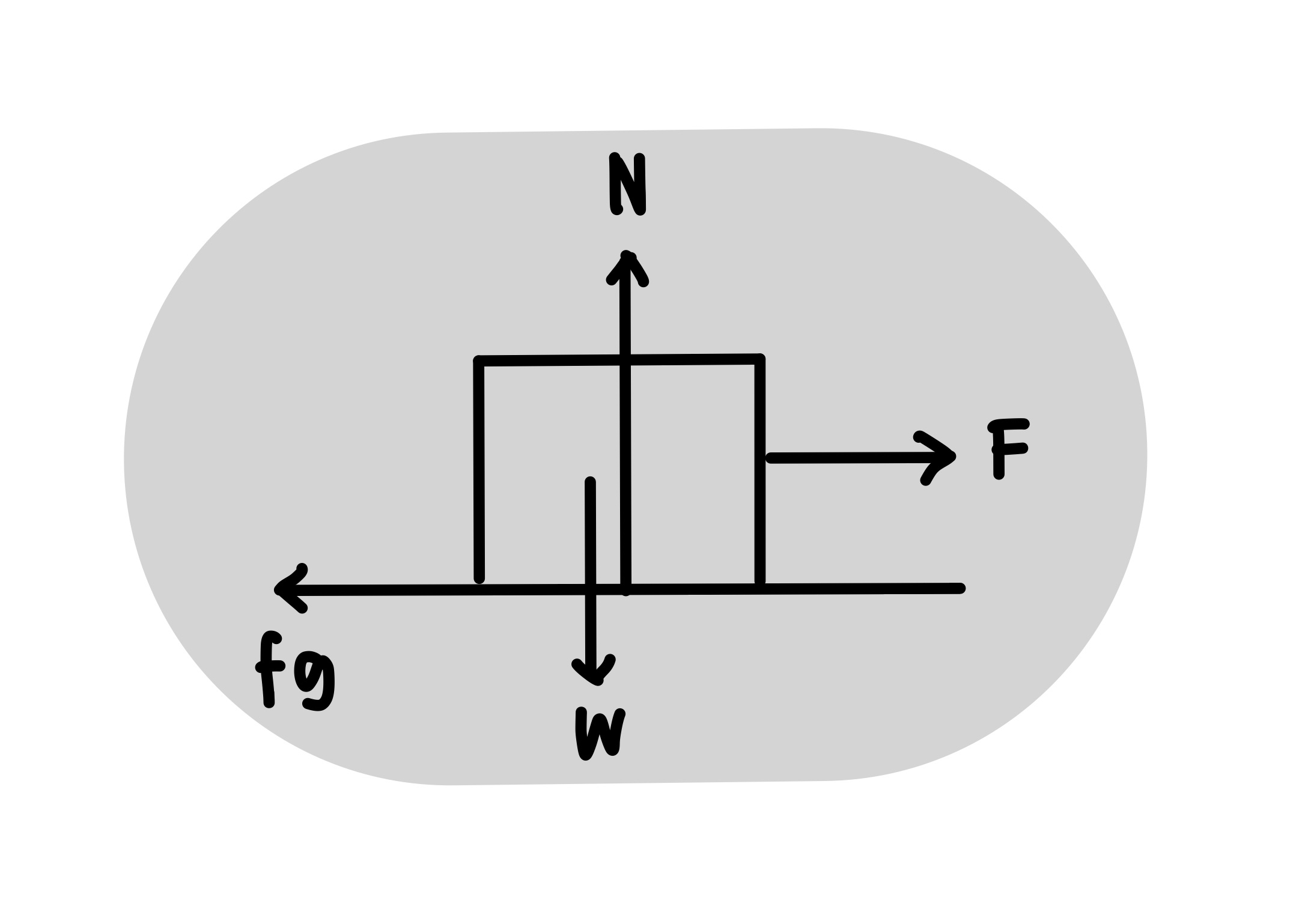
F = gaya tarik (N)
`f_{g}`= gaya gesekan (N)
m = massa benda (kg)
a = percepatan (m/`s^{2}`)
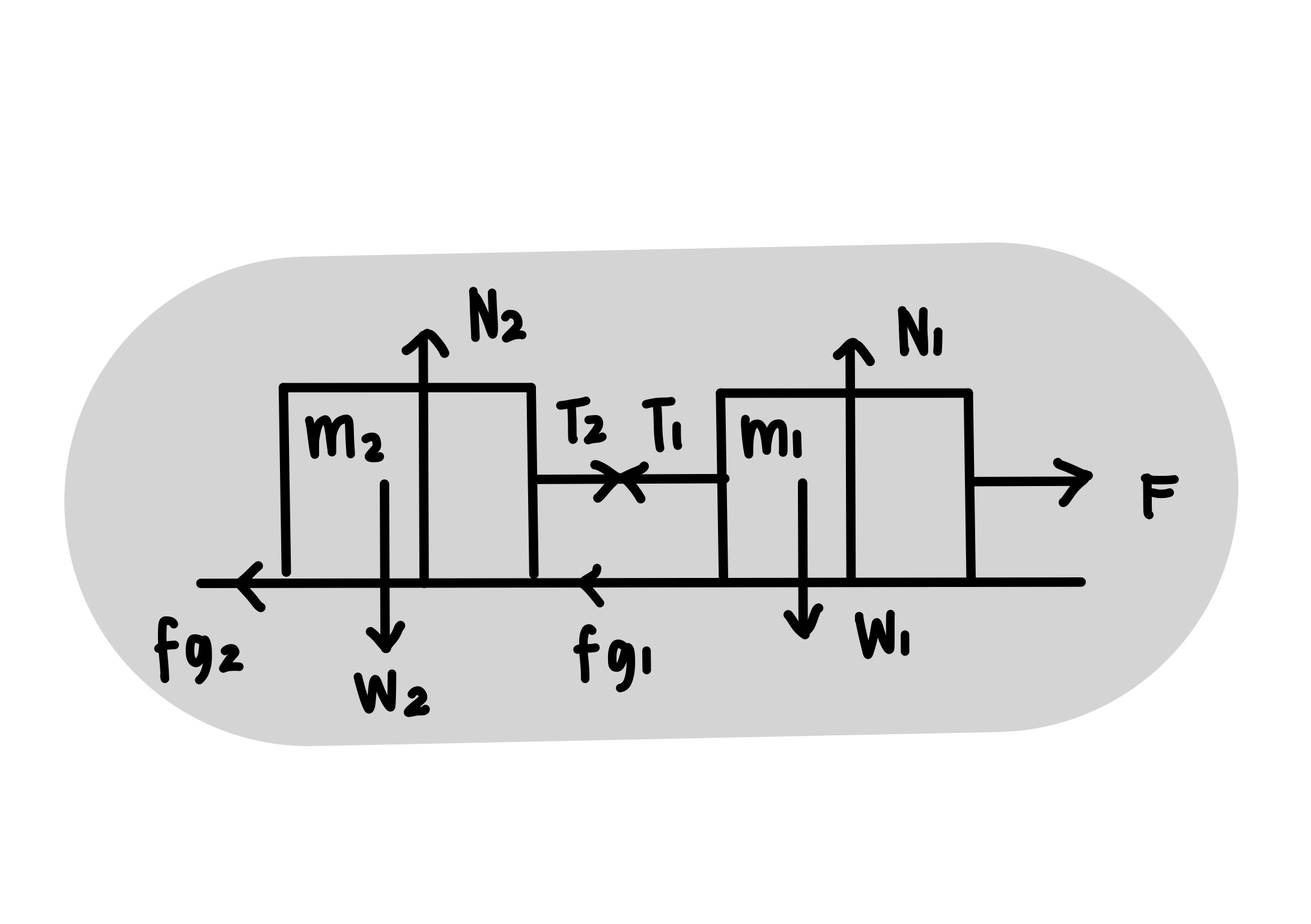
F = gaya tarik (N)
`f_{g1}`= gaya gesekan benda 1(N)
`f_{g2}`= gaya gesekan benda 2 (N)
`m_{1}` = massa benda 1 (kg)
`m_{2}` = massa benda 2 (kg)
a = percepatan (m/`s^{2}`)
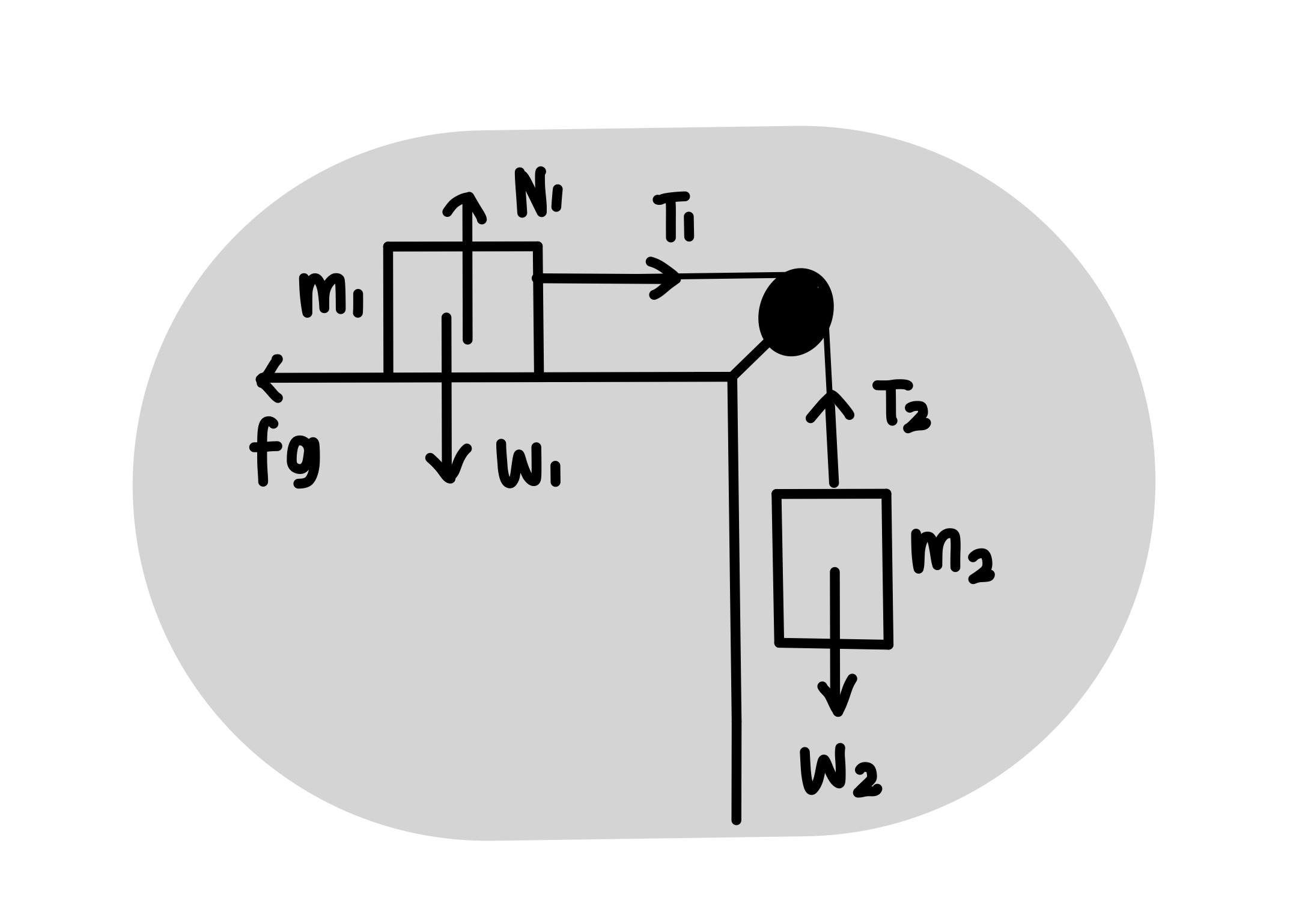
`w_{1}` = berat benda 1 (kg)
`w_{2}` = berat benda 2 (kg)
`f_{g}`= gaya gesekan benda 1 (N)
`m_{1}` = massa benda 1 (kg)
`m_{2}` = massa benda 2 (kg)
a = percepatan (m/`s^{2}`)
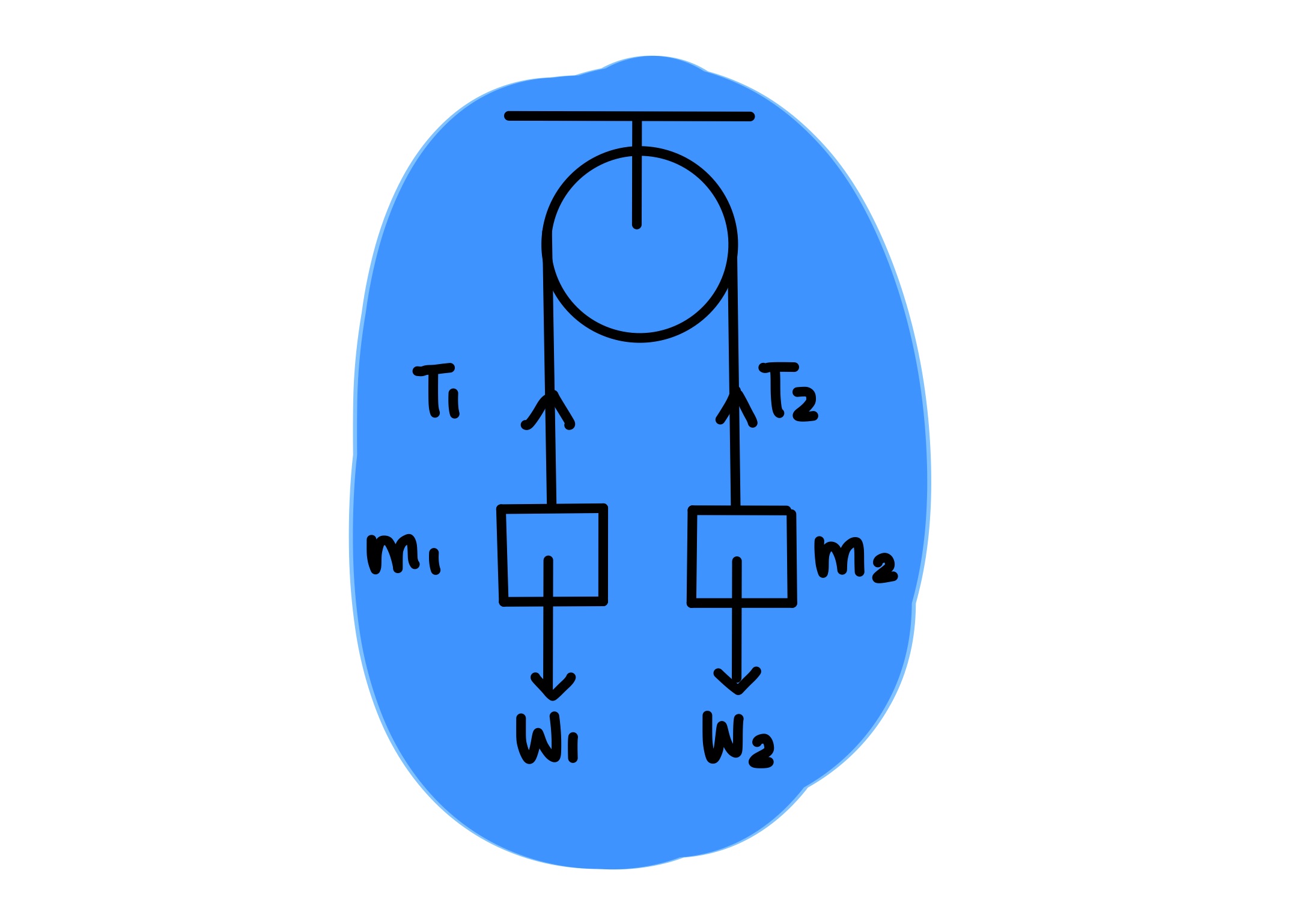
`w_{1}` = berat benda 1 (kg)
`w_{2}` = berat benda 2 (kg)
`m_{1}` = massa benda 1 (kg)
`m_{2}` = massa benda 2 (kg)
a = percepatan (m/`s^{2}`)
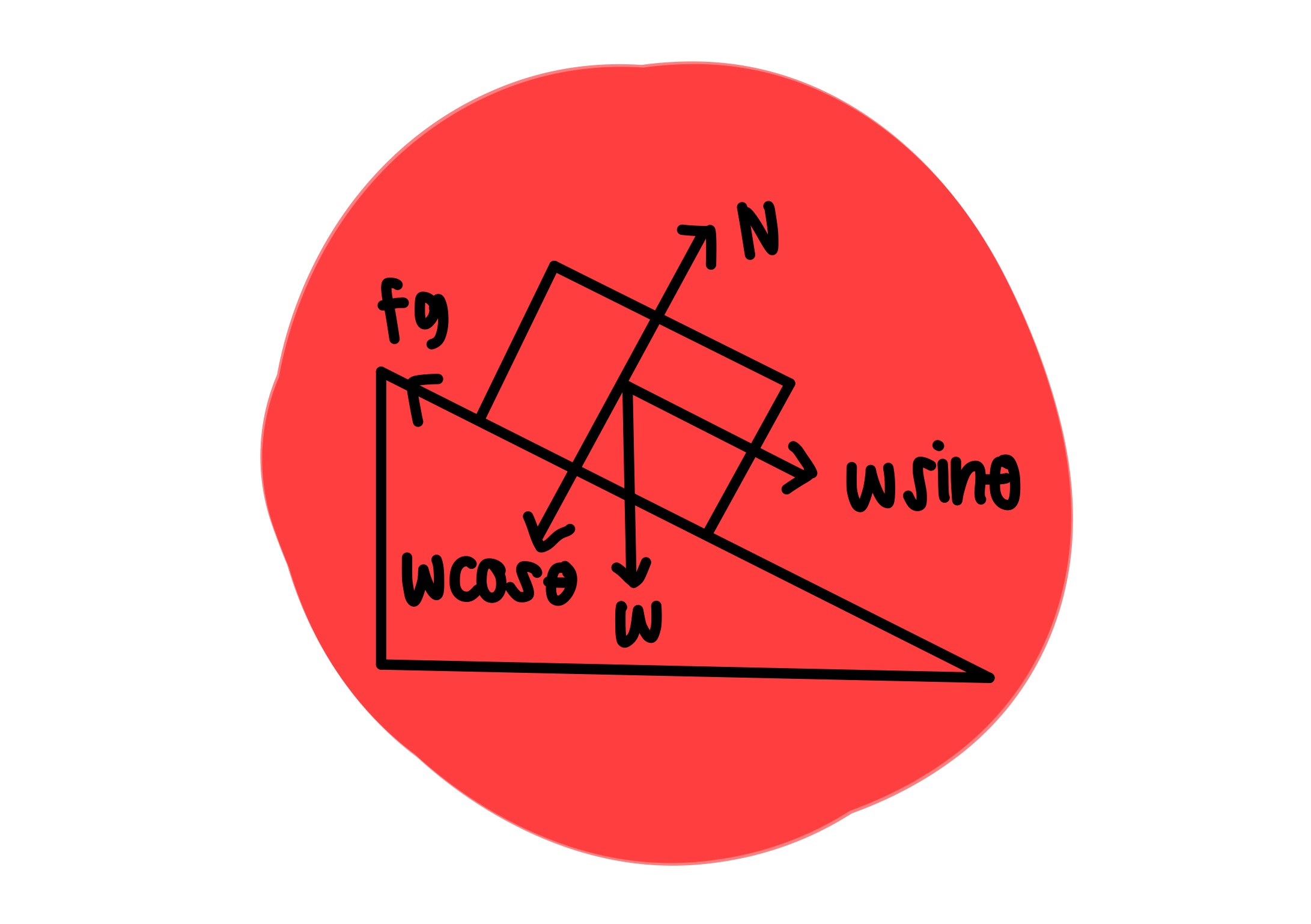
w = berat benda (N)
`\theta` = sudut kemiringan benda
`f_{g}` = gaya gesekan (N)
m = massa benda (kg)
a = percepatan (m/`s^{2}`)
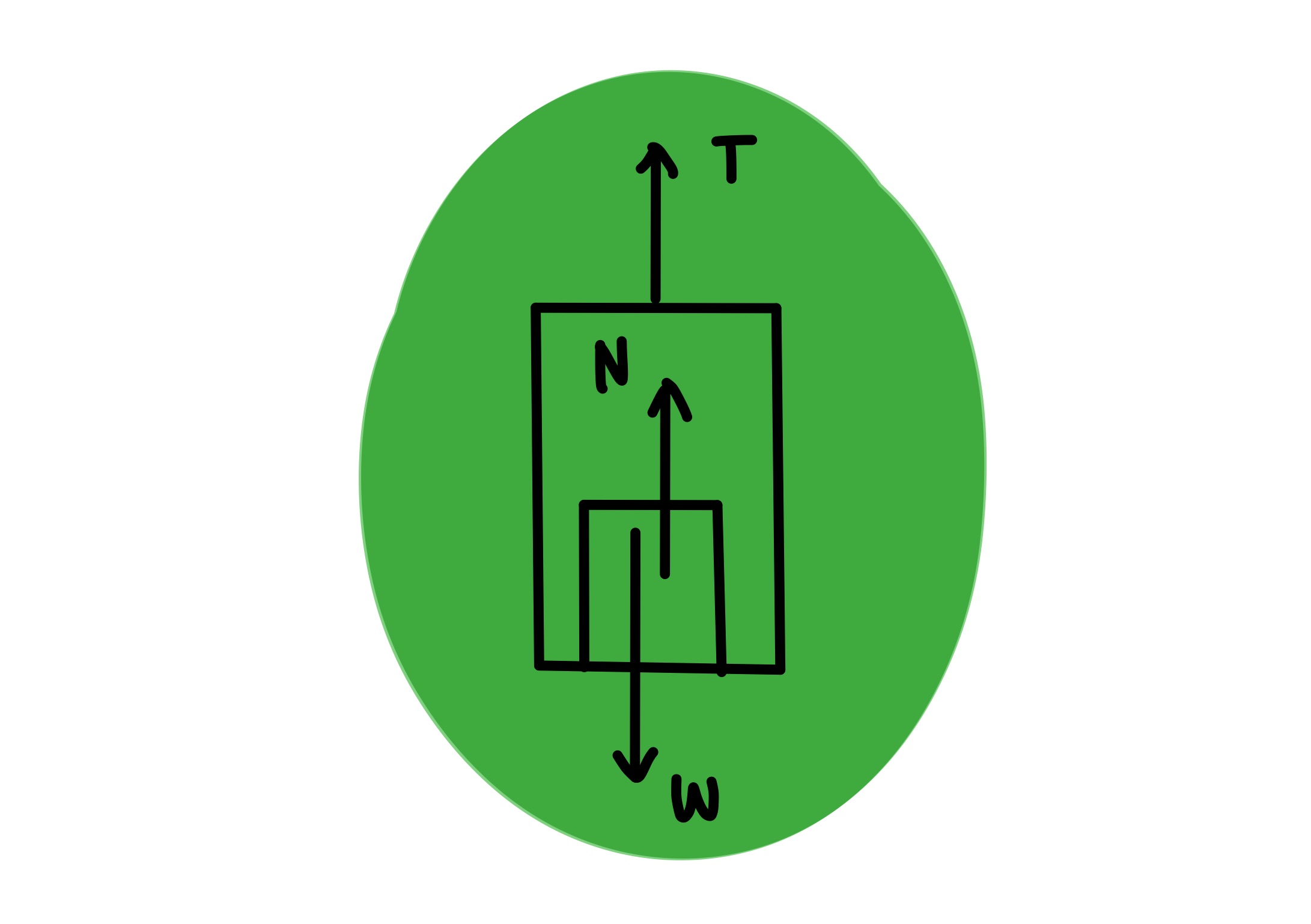
w = gaya berat (N)
N = gaya normal (N)
m = massa orang atau benda dalam lift(kg)
a = percepatan (m/`s^{2}`)
Pada Bab Gravitasi, siswa akan mempelajari tentang gaya gravitasi dan pengaruh gravitasi terhadap gerak planet yang dijelaskan dalam Hukum Keppler.
F = gaya tarik menarik antara kedua benda (N)
`m_{1}`= massa benda 1 (kg)
`m_{2}`= massa benda 2 (kg)
r = jarak antara kedua pusat benda (m)
G = tetapan gravitasi universal
(`6,67\times 10^{-11}N.m^{2}/kg^{2}`)
g = medan gravitasi atau percepatan gravitasi (m/`s^{2}`)
G = tetapan gravitasi universal
(`6,67\times 10^{-11}N.m^{2}/kg^{2}`)
M = massa dari suatu planet atau benda (kg)
r = jari-jari dari suatu planet(m)
Apabila terdapat planet `m_{A}` dan `m_{B}` serta memiliki jari-jari `R_{A}` dan `R_{B}`, perbandingan antara percepatan gravitasi planet A dan B dapat dinyatakan dalam rumus seperti di atas.
G = tetapan gravitasi universal
(`6,67\times 10^{-11}N.m^{2}/kg^{2}`)
M = massa benda yang menghasilkan medan gravitasi
r = jarak (m)
T = kala revolusi suatu planet (s atau tahun)
R = jarak suatu planet ke matahari (m atau sa)
Atau pada bidang miring,
W = usaha (joule)
F = gaya yang sejajar dengan perpindahan (N)
s = perpindahan (m)
`\alpha` = sudut kemiringan
W = usaha/energi (joule)
t = waktu (s)
P = daya (joule/sekon) atau (watt)
Ketika ada benda A dan benda B
`E_{p}`= energi potensial (joule)
m = massa (kg)
g = percepatan gravitasi (m/`s^{2}`
h = ketinggian terhadap titik acuan (m)
m = massa (kg)
v = kecepatan (m/s)
`v_{2}` = kecepatan akhir (m/s)
`v_{1}` = kecepatan awal (m/s)
`h_{2}` = ketinggian kedua (m)
`h_{1}` = ketinggian pertama (m)
Momentum adalah hasil kali massa dan kecepatan vektor suatu benda, sedangkan impuls merupakan hasil perkalian antara gaya dengan selang waktu.
p = momentum (kg.m/s)
m = massa benda (kg)
v = kecepatan (m/s)
I = impuls (N.s = kg.m/s)
F = gaya yang diberikan (N)
`\Deltat`= selang waktu (s)
Dapat dikatakan bahwa
Sehingga,
Jika benda bergerak ke kiri maka nilai v bernilai negatif (-)
Jika benda bergerak ke kanan maka nilai v bernilai negatif (+)
p' = momentum benda sebelum tumbukan
v = kecepatan benda sebelum tumbukan
p' = momentum benda setelah tumbukan
v = kecepatan benda setelah tumbukan
Gerak harmonik merupakan gerak periodik yang paling dasar dari berbagai jenis gerak periodik.
Karena `\theta=\omega.t` maka,
y = simpangan (m)
A = amplitudo atau simpangan terjauh (m)
`\theta` = sudut fase
`\omega` = frekuensi sudut (rad/s)
[`omega=2\pi.f`]
t = waktu bergetar (s)
Sehingga
Dengan,
m = massa benda (kg)
k = konstanta pegas (N/m)
`l` = panjang tali (m)
g = percepatan gravitasi (m/`s^{2}`)
m = massa benda (kg)
A = amplitudo (m)
`\omega` = kecepatan sudut (rad/s)
t = waktu (sekon)
A = amplitudo (m)
y = simpangan (m)
k = konstanta pegas (N/m)
Rumus Umum energi mekanik
Maka energi mekanik pada gerak harmonik dapat dirumus sebagai berikut